LeetCode 124. Binary Tree Maximum Path Sum

124. Binary Tree Maximum Path Sum

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node’s values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

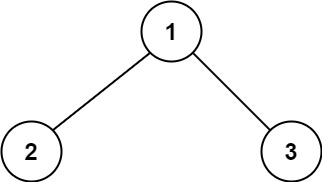
Example 1:

Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

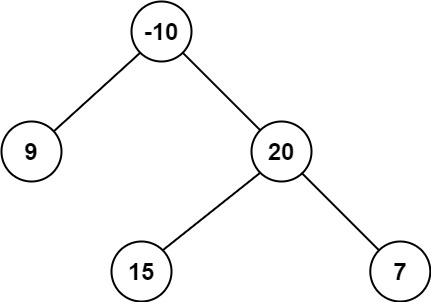
Example 2:

Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

Solution

Try to reduce the problem to gain some insights. What if we were actually dealing with a Linked List instead of a tree. What if it was actually an array and we were asked to find the path with maximum sum ? That would be the subarray with maximum sum. That kind of sounds like 53. Maximum Subarray. Although our is technically different than Maximum Subarray problem it is analogous.

For any node, can we find the path with the maximum sum that includes the current node ?

If we can, then we can do it for every node and find the answer. Now how would we find an optimal path for a given node ?

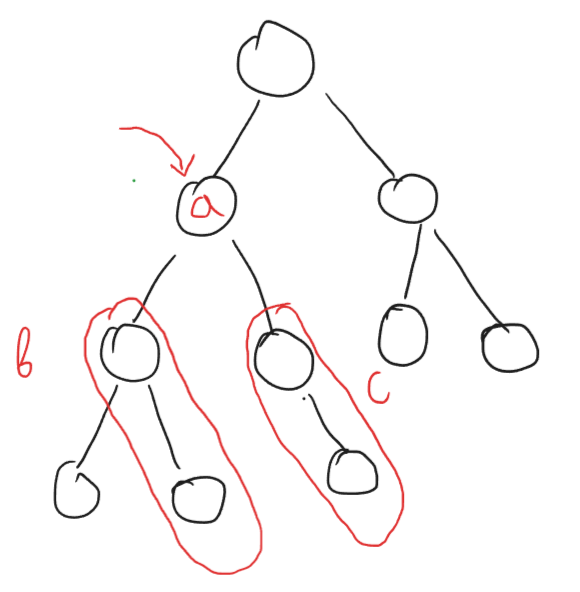
Let me depict it for an example.

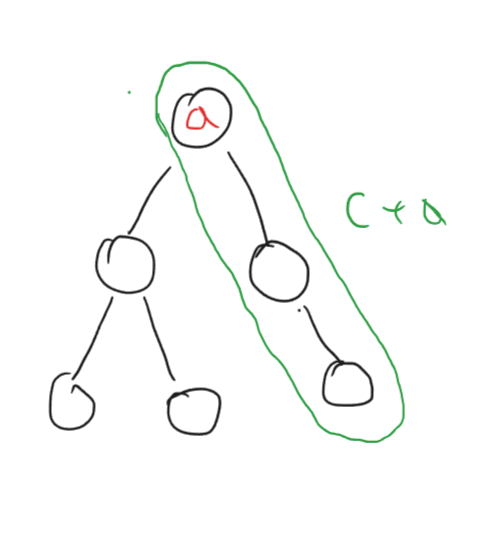
Suppose we want to find the path with the maximum sum that includes the root node with value a in the picture. What do we need to know ?

Let’s assume we know the optimal vertical path (a path that does not bend at a root node) of the left and the right subtrees. These paths are shown in the picture with left subtree having a path sum of b and right subtree having a path sum of c.

What would the optimal path look like for the root node a?

There are a few cases we have to consider. Let’s see them one by one

The first case

The optimal path for the root node a includes the optimal vertical path of the left subtree.

By optimal vertical path, we mean a path with maximum sum that starts at a root node and travels down, ending at another node. For example optimal vertical path of the left subtree is the path with maximum sum that starts at the root of the left subtree and ends at a leaf node in this case.

The second case

The optimal path for the root node a includes the optimal vertical path of the right subtree.

The third case

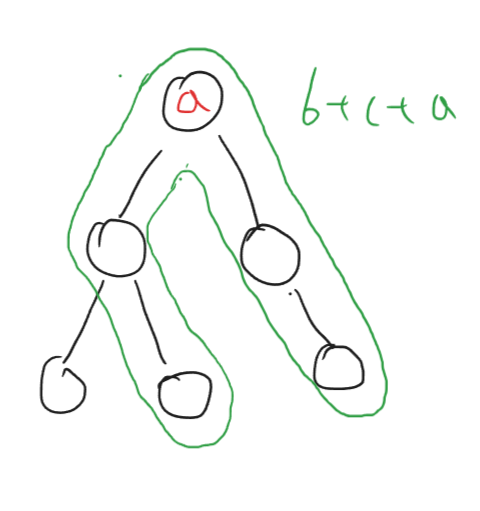
The optimal path for the root node a includes both the optimal vertical path of the left and right subtrees.

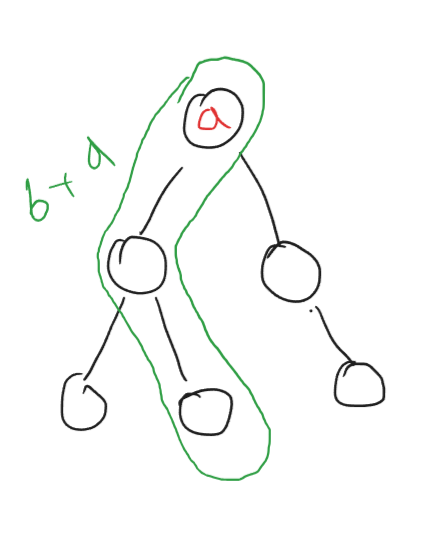
In case the sum of optimal vertical paths of left and right subtrees is negative, meaning b < 0 and c < 0. Then we would get a better result by not including these sums. This case is given below

The fourth case

As you can see, we only include the root node itself while excluding the sums of the left and right subtrees.

In case if the root node itself holds a negative value, meaning a < 0, then we can actually exlude it as well. This means that the subtree rooted at node with value a does not have any path with positive path sum.

For the parent of our node with value a, we will return a value that will denote the optimal vertical path with maximum sum that starts at the current node a. This path would be one of the paths from the first, second and fourth cases. You can look at them again. If none of these paths has a positive path sum, we will return 0 to the parent node.

Now let’s look at the code.

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
#define vv std::vector
#define pp std::pair


static int speedup = [](){std::ios_base::sync_with_stdio(false); std::cin.tie(NULL); return 1;}();

class Solution {
public:
    int maxPathSum(TreeNode* root) {
        sum = INT_MIN;
        auto p = dfs(root);
        return sum;
    }

private:
    int sum = INT_MIN;
    int dfs(TreeNode* root)
    {
        if(root == NULL)
            return 0;
        int left = dfs(root->left); //optimal vertical path of left subtree
        int right = dfs(root->right); // and the right subtree
        int x = left + root->val; // first case (look at the pictures)
        int y = right + root->val; // second case
        //we update the current sum. left + right + root->val is the third case
        sum = std::max({sum, left + right + root->val, x, y});
        //the value of the optimal vertical path to return to the parent
        int a = std::max({root->val, x, y});
        //if all of them have negative path sums, return 0
        return std::max(a, 0);
    }

};

I hope you enjoyed this article. Come back for more!